前言
解数独是刚接触程式时的第一份作业,当时有很多想法,自己写不太出来,也找不太到一步步讲解相关想法的实作,所以想以数独作为写 blog 的开始,希望有机会帮助需要的人。
另外,非常欢迎路过的有缘人提出建议啦~ 无论变数命名、内容设计或是定位,任何东西都欢迎提噢!
解法一: 传统 Backtracking
这大概是最常见的解法,backtracking 的精神就不在此赘述,大概就是按照一定的顺序进行试错(trial and error),若某一步走不下去了便返回上一步继续之前的试错
以下为使用此法求解数独的过程: gif 来源
![]()
1
2
3
#define N 9
int ans_count;
int sudoku[N][N];
sudoku[N][N]储存 9x9 格的数字,0表示空白。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
void next_bt(int r, int c)
{
c == N-1 ? bt(r+1, 0) : bt(r, c+1);
}
void bt(int r, int c)
{
if (r == N) {
ans_count++;
sudoku_print();
return;
}
if (sudoku[r][c] != 0)
next_bt(r, c);
else {
for (int n = 1; n <= N; ++n) {
if (can_fill(r, c, n)) {
sudoku[r][c] = n;
next_bt(r, c);
sudoku[r][c] = 0;
}
}
}
}
// call bt(0, 0) to solve
next_bt(r, c) 由左至右,由上而下,依序进行试错
bt(r, c) 对数独的第 r row, 第 c col试错
原本看到
next_bt(r, c)这种只有一两行的 funcion 想说加上 inline 减少 call function 的 overhead 来加快速度,实测上也确实有微小的加速,但 GNU 自带的 optimization flag 增快的幅度会是以倍数来计算的,而加上 inline 的优化后反而慢了一点……所以如果可以自行 compile 或许就不用考虑用 inline 来加速吧。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
bool can_fill_row(int r, int n)
{
for (int c = 0; c < N; ++c)
if (sudoku[r][c] == n)
return false;
return true;
}
bool can_fill_col(int c, int n)
{
for (int r = 0; r < N; ++r)
if (sudoku[r][c] == n)
return false;
return true;
}
bool can_fill_box(int r, int c, int n)
{
int r_start = r/3 * 3;
int c_start = c/3 * 3;
for (int i = r_start; i < r_start+3; ++i)
for (int j = c_start; j < c_start+3; ++j)
if (sudoku[i][j] == n)
return false;
return true;
}
bool can_fill(int r, int c, int n)
{
return can_fill_row(r, n) && can_fill_col(c, n) && can_fill_box(r, c, n);
}
can_fill_row(r, n)寻找第 r row是否已存在数字 n,以此类推。
box 表示数独中的宫 (小 3x3)。
第 19 行 r_start = r/3 * 3 取得 r 所在之宫的 row 起始位置,c_start 同理。
解法二: 优化版 Backtracking
解法一的 can_fill(r, c, n) 每次都要重新看过空白处所在之行、列、宫是否存在数字n,而这件事只会在数独更动时才会有变化,因此可以通过新增一些变数来实时记录。(非常经典的空间换时间)
1
2
3
bool row[N][N+1];
bool col[N][N+1];
bool box[N][N+1];
row[r][n] 表示第 r row 是否存在数字 n,以此类推。
1
2
3
4
5
6
7
8
9
int get_box(int r, int c)
{
return r/3*3 + c/3;
}
bool can_fill(int r, int c, int n)
{
return !row[r][n] && !col[c][n] && !box[get_box(r,c)][n];
}
get_box(r, c) 找到 r, c 对应的 box 编号。编号由左至右,由上而下,依序为 0-8。其对应关系通过尝试几组 r, c 不难发觉。
于是,原本 O(n) 的 can_fill(r, c, n) 就可以在 O(1) 时间内完成了!(虽然原本的 O(n) 的 n 也只是 9)
Big O notation
更改数独时同步更新变数
也就是将解法一的 bt(r, c) 中的
1
2
3
sudoku[r][c] = n;
next_bt(r, c);
sudoku[r][c] = 0;
替换为
1
2
3
fill(r, c, n);
next_bt(r, c);
erase(r, c, n);
其中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void do_fill(int r, int c, int n, bool b)
{
row[r][n] = b;
col[c][n] = b;
box[get_box(r,c)][n] = b;
sudoku[r][c] = b ? n : 0;
}
void fill(int r, int c, int n)
{
do_fill(r, c, n, true);
}
void erase(int r, int c, int n)
{
do_fill(r, c, n, false);
}
解法三: 初步拟人
解法一、二虽然可行,但每一步都用猜的,具不确定性,而很多时候有些空白处就只能填一个数字。(是确定的)
若每次都先填入这些已知正确的数字,就可以减少很多不必要的尝试。
在较难的数独上,我们也会遇到瓶颈(每个空白处都有超过一个数字可填),这时可以选择一个空白处进行试错后,再重复本解法。(有一点点Backtracking的感觉)
这就好像先把所有确定的格子填好后发现做不下去,只好影印一份,先在影本猜其中一格再继续往下做。
当然就算是已经有一个格用猜的影本也可能出现做不下去的情况,这时就需要将这影本拿去影印,去尝试解这影本的影本。
啰嗦几句,为什么要拿去影印呢?
举个例子,当我们遇到瓶颈时,若先尝试在某一格填入数字 2,解一解发现无解(某空白处无法被填入任何数字),这表示刚刚猜的数字 2 是错误的,那么假设没有事先影印,就没办法恢复到之前的状态了。
先以 pseudo code 的方式呈现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
solve(Sudoku s)
{
do {
for each empty cell of Sudoku s {
若只能填唯一数字则填之 // 若在此处发现没有可填数表示此 Sudoku s 无解
}
} while (这一次 loop 有找到可填数字); // 若1个完整 loop 找不到任何数字可填,
// 那么就算再 loop 几次也不会有结果
if (没空白处了) {
输出解
} else {
for each 第一个空白处的可填数字 n:
s' <- s 填入 数字n
solve(s')
}
}
这种解法有可能同时存在多个数独,所以不能再用全域变数打天下了,先定义
1
2
3
4
5
6
typedef struct _Sudoku{
int grid[N][N];
bool row[N][N+1];
bool col[N][N+1];
bool box[N][N+1];
} Sudoku;
主体
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
void sudoku_solve(Sudoku *thiz)
{
int num_filled, num_unsolved;
do {
num_filled = 0;
num_unsolved = 0;
FOR_FOR_EACH_EMPTY_CELL(r, c, thiz) {
int num_can_fill = 0;
int nn;
FOR_EACH_NUM(n) {
if(sudoku_can_fill(thiz, r, c, n)) {
num_can_fill++;
nn = n;
if (num_can_fill > 1) // pruning
break;
}
}
if (num_can_fill == 0) // no solution
return;
if (num_can_fill == 1) {
sudoku_fill(thiz, r, c, nn);
num_filled++;
} else
num_unsolved++;
}
} while (num_filled != 0);
if (num_unsolved == 0) {
ans_count++;
sudoku_print(thiz);
} else {
// find the first empty cell, try to fill and solve it
FOR_FOR_EACH_EMPTY_CELL(r, c, thiz) {
FOR_EACH_NUM(n) {
if (sudoku_can_fill(thiz, r, c, n)) {
Sudoku sudoku_tmp;
memcpy(&sudoku_tmp, thiz, sizeof(Sudoku));
sudoku_fill(&sudoku_tmp, r, c, n);
sudoku_solve(&sudoku_tmp);
}
}
return;
}
}
}
小 function 们都与之前的类似,只是新增对哪个 sudoku 做操作。比如 sudoku_can_fill(thiz, r, c, n) 和 can_fill(r, c, n) , 前者表示针对数独 thiz 检查位置 r, c 能否填入 n 。
其中
1
2
3
#define FOR_N(i) for (int i = 0; i < N; ++i)
#define FOR_FOR_EACH_EMPTY_CELL(r, c, s) FOR_N(r) FOR_N(c) if(s->grid[r][c] == 0)
#define FOR_EACH_NUM(n) for (int n = 1; n <= N; ++n)
由于有些地方遍历 0-8,有些则遍历 1-9,为了减少不必要的 bug,将其定义为 macro
解法四: 环保拟人
每次遇到瓶颈都要复制一整个 Sudoku (9×9=81 int + 3×9×10=270 bool),好像没必要?
解法三中,影印的比喻是为了配合程式实作上的便利,我想实际上一般人不会这么做。通常(在无法推理又想解出来时)大家会用原子笔填入确定解,而不确定的部分改用铅笔填写,发现错了就把用铅笔填的擦掉。(用铅笔之后又遇到瓶颈时就想象用更浅的铅笔来填)
我们可以运用 stack 来保留每一轮填下的数字。
这种做法实际上会稍微慢一点点(维护 stack 需要时间成本),但好处是就算一直遇到瓶颈也只会存在一份数独。
以下借用 C++ 的 stack 来完成
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
void do_sudoku_solve(Sudoku *thiz, stack<Cell> *s, bool record)
{
int num_filled, num_unsolved;
do {
num_filled = 0;
num_unsolved = 0;
FOR_FOR_EACH_EMPTY_CELL(r, c, thiz) {
int num_can_fill = 0;
int t;
FOR_EACH_NUM(n) {
if(sudoku_can_fill(thiz, r, c, n)) {
num_can_fill++;
t = n;
if (num_can_fill > 1) // pruning
break;
}
}
if (num_can_fill == 0) // no solution
return;
if (num_can_fill == 1) {
sudoku_fill(thiz, r, c, t);
num_filled++;
if (record) {
Cell cell = {.r=r, .c=c, .n=t};
s->push(cell);
}
} else
num_unsolved++;
}
} while (num_filled != 0);
if (num_unsolved == 0) {
ans_count++;
sudoku_print(thiz);
} else {
// find the first empty cell, try to fill and solve it
FOR_FOR_EACH_EMPTY_CELL(r, c, thiz) {
FOR_EACH_NUM(n) {
if (sudoku_can_fill(thiz, r, c, n)) {
sudoku_fill(thiz, r, c, n);
sudoku_solve(thiz, true);
sudoku_erase(thiz, r, c, n);
}
}
return;
}
}
}
void sudoku_solve(Sudoku *thiz, bool record=false)
{
stack<Cell> s;
do_sudoku_solve(thiz, &s, record);
while(!s.empty()) {
Cell cell = s.top();
sudoku_erase(thiz, cell.r, cell.c, cell.n);
s.pop();
}
}
record default 为 false 是因为第一次不用记录(所有答案都是确定正确的)
可以发现第 40 行处不需要像 解法三 一样复制整个数独了
原本想说这部分只写成一个 function(感觉比较完整?),但
do_sudoku_solve共有三个有可能 return 的地方(19、44、47行),不知若要在 return 前把 stack 里记录的数字erase掉,是要利用 goto 好呢,还是像这样拆成两个 function 呢?又或是有其它解法呢?
解法五: 四角拟人
只有某格只能填一个数字时才能确定该格的解?
其实还有很多情况,比如在某一行中,某个数字就只能填在该行某一空白处时,则该数字为该空白处的解。
同理,以列和宫的角度出发也一样。
也就是说,我们除了以格的角度(某空白处只能填一个数字)来寻解之外,亦可以行、列、宫的角度来观察。
而每个观察角度的求解能力(可得出解之空白处集合)是不同的,大约如下图所示:
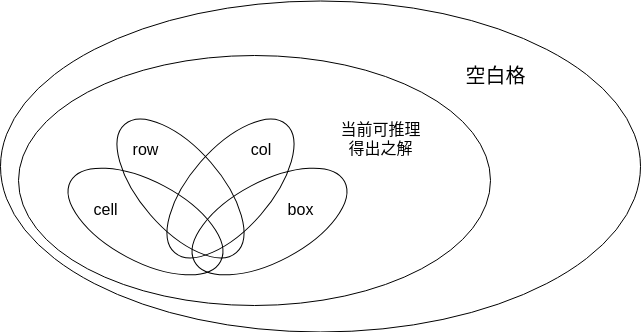
图中 row 集合表示以 row 的角度来观察可得出解之空白处集合, col、box、cell 同理
Venn diagram with n = 4
此图进一步解释
因此用越多角度来观察越有机会降低试错的次数,但这也造成一定的 overhead,具体哪种解法比较快因数独难度而异。
解法五中,我们从行、列、宫、格四种角度寻解。新增三种角度寻找的过程与以格的角度(参考解法三)类似,于是写成 乱乱的 macro。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
#define FOR_3(k, start) for (int kk = start, k = kk; k < kk+3; ++k)
#define FOR_R_C_IN_BOX(r, c, i) FOR_3(r, get_r(i)) FOR_3(c, get_c(i))
#define FILL_IF_EXACTLY_ONE(LOOP1, LOOP2, save_tmp, sudoku_fill_stmt) \
do { \
LOOP1 { \
int num_can_fill = 0; \
LOOP2 { \
if (sudoku_can_fill(thiz, r, c, n)) { \
num_can_fill++; \
save_tmp; \
if (num_can_fill > 1) /* pruning */ \
break; \
} \
} \
if (num_can_fill == 0) \
return false; \
if (num_can_fill == 1) { \
sudoku_fill_stmt; \
++*num_filled; \
} else if (count_unsolved) \
++*num_unsolved; \
} \
return true; \
} while (0)
bool sudoku_solve_row(Sudoku *thiz, int *num_filled, int *num_unsolved, bool count_unsolved)
{
int cc;
FILL_IF_EXACTLY_ONE(
FOR_N(r) FOR_EACH_NUM(n) if(!thiz->row[r][n]),
FOR_N(c) if(!thiz->grid[r][c]),
cc = c,
sudoku_fill(thiz, r, cc, n)
);
}
bool sudoku_solve_col(Sudoku *thiz, int *num_filled, int *num_unsolved, bool count_unsolved)
{
int rr;
FILL_IF_EXACTLY_ONE(
FOR_N(c) FOR_EACH_NUM(n) if(!thiz->col[c][n]),
FOR_N(r) if(!thiz->grid[r][c]),
rr = r,
sudoku_fill(thiz, rr, c, n)
);
}
bool sudoku_solve_box(Sudoku *thiz, int *num_filled, int *num_unsolved, bool count_unsolved)
{
int rr, cc;
FILL_IF_EXACTLY_ONE(
FOR_N(i) FOR_EACH_NUM(n) if(!thiz->box[i][n]),
FOR_R_C_IN_BOX(r, c, i) if(!thiz->grid[r][c]),
rr = r; cc = c,
sudoku_fill(thiz, rr, cc, n)
);
}
bool sudoku_solve_cell(Sudoku *thiz, int *num_filled, int *num_unsolved, bool count_unsolved)
{
int nn;
FILL_IF_EXACTLY_ONE(
FOR_FOR_EACH_EMPTY_CELL(r, c, thiz),
FOR_EACH_NUM(n),
nn = n,
sudoku_fill(thiz, r, c, nn)
);
}
void sudoku_solve(Sudoku *thiz)
{
int num_filled, num_unsolved;
do {
num_filled = 0;
num_unsolved = 0;
if (!sudoku_solve_row(thiz, &num_filled, &num_unsolved, false) ||
!sudoku_solve_col(thiz, &num_filled, &num_unsolved, false) ||
!sudoku_solve_box(thiz, &num_filled, &num_unsolved, false) ||
!sudoku_solve_cell(thiz, &num_filled, &num_unsolved, true))
return;
} while (num_filled != 0);
if (num_unsolved == 0) {
ans_count++;
sudoku_print(thiz);
} else {
// find the first empty cell, try to fill and solve it
FOR_FOR_EACH_EMPTY_CELL(r, c, thiz) {
FOR_EACH_NUM(n) {
if (sudoku_can_fill(thiz, r, c, n)) {
Sudoku sudoku_tmp;
memcpy(&sudoku_tmp, thiz, sizeof(Sudoku));
sudoku_fill(&sudoku_tmp, r, c, n);
sudoku_solve(&sudoku_tmp);
}
}
return;
}
}
}
Why use apparently meaningless do-while statements in macros
再次强调,上述四种观察角度,单用任何一种或是混合使用都可以在有限时间内求解简单数独。
解法六: 优先试错
遇到瓶颈时,针对哪个空白处进行试错最佳呢?
答案大概很复杂,但我们可以用很简单的方式找到较佳的位置:最少可填数的空白处
原因是平均来说需要较少的试错就能找到该格子的正解
实作上很简单,只需将 解法五 的最后部分替换为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
int Min = N;
int r_min = 0, c_min = 0;
// find the empty cell with fewest possible answer
FOR_FOR_EACH_EMPTY_CELL(r, c, thiz) {
int num_can_fill = 0;
FOR_EACH_NUM(n) {
if (sudoku_can_fill(thiz, r, c, n)) {
++num_can_fill;
}
}
if (num_can_fill < Min) {
Min = num_can_fill;
r_min = r;
c_min = c;
}
}
// try to fill and solve it
FOR_EACH_NUM(n) {
if (sudoku_can_fill(thiz, r_min, c_min, n)) {
Sudoku sudoku_tmp;
memcpy(&sudoku_tmp, thiz, sizeof(Sudoku));
sudoku_fill(&sudoku_tmp, r_min, c_min, n);
sudoku_solve(&sudoku_tmp);
}
}
解法七: 格格加速
检查某数是否可以填入某格虽然已经做到 O(1),但寻解时要确定某格是否只能填入一个数字,目前还是需要逐个数字检查,时间为 O(n)。
与 解法二 的优化同理,某格可填数的个数只会在所在之行、列、宫有更动时才会改变。因此我们同样可以再储存这些资讯来避免每次重新计算。
1
2
3
4
5
6
7
8
typedef struct _Sudoku {
int grid[N][N];
bool row[N][N+1];
bool col[N][N+1];
bool box[N][N+1];
bool can_fill[N][N][N+1];
int num_can_fill_cell[N][N];
} Sudoku;
can_fill[r][c][n] 表示第 r row 第 c col 是否可填入数字 n
num_can_fill_cell[r][c] 表示第 r row 第 c col 可填数字个数
这样一来,确定某格可填数个数的过程也变 O(1) 了!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
bool sudoku_solve_cell(Sudoku *thiz, int *num_filled, int *num_unsolved, bool count_unsolved)
{
FOR_FOR_EACH_EMPTY_CELL(r, c, thiz) {
if (thiz->num_can_fill_cell[r][c] == 1) {
FOR_EACH_NUM(n) {
if (sudoku_can_fill(thiz, r, c, n)) {
sudoku_fill(thiz, r, c, n);
++*num_filled;
break;
}
}
} else if (thiz->num_can_fill_cell[r][c] == 0) {
return false; // pruning
} else if (count_unsolved) {
++*num_unsolved;
}
}
return true;
}
平时确定某数是否可填入某格也能稍稍加速,
1
2
3
4
bool sudoku_can_fill(Sudoku *thiz, int r, int c, int n)
{
return thiz->can_fill[r][c][n];
}
但原本的版本还是有必要存在的(真正具有判断能力,更新 thiz->can_fill 时需要)
1
2
3
4
bool sudoku_can_fill_2(Sudoku *thiz, int r, int c, int n)
{
return !thiz->row[r][n] && !thiz->col[c][n] && !thiz->box[get_box(r,c)][n];
}
更动某格会影响所在之行、列、宫的状态
从这里也可以看出,为了实时更新可填状态,更动某格所需时间从原本的 O(1) 变成 O(n) 了,但大部分情况下搜索的次数远大于更动的次数,所以这代价还是值得的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
bool sudoku_maybe_update_can_fill(Sudoku *thiz, int r, int c, int n, bool fill)
{
if (fill) {
if (thiz->can_fill[r][c][n] == true) {
thiz->can_fill[r][c][n] = false;
thiz->num_can_fill_cell[r][c]--;
}
} else {
if (thiz->can_fill[r][c][n] == false &&
sudoku_can_fill_2(thiz, r, c, n)) {
thiz->can_fill[r][c][n] = true;
thiz->num_can_fill_cell[r][c]++;
}
}
}
void do_sudoku_fill(Sudoku *thiz, int r, int c, int n, bool fill)
{
const int box_index = get_box(r, c);
thiz->row[r][n] = fill;
thiz->col[c][n] = fill;
thiz->box[box_index][n] = fill;
thiz->grid[r][c] = fill ? n : 0;
FOR_N(rr) {
sudoku_maybe_update_can_fill(thiz, rr, c, n, fill);
}
FOR_N(cc) {
sudoku_maybe_update_can_fill(thiz, r, cc, n, fill);
}
FOR_R_C_IN_BOX(rr, cc, box_index) {
sudoku_maybe_update_can_fill(thiz, rr, cc, n, fill);
}
}
解法六的优化过程也可以简化为
1
2
3
4
5
6
7
FOR_FOR_EACH_EMPTY_CELL(r, c, thiz) {
if (thiz->num_can_fill_cell[r][c] < Min) {
Min = thiz->num_can_fill_cell[r][c];
r_min = r;
c_min = c;
}
}
解法八: 全面加速
解法七中对格的优化同样适用于其他三种角度中
我想到此为止大概是 array 能做到的极限了吧(?)
1
2
3
4
5
6
7
8
9
10
11
typedef struct _Sudoku {
int grid[N][N];
bool row[N][N+1];
bool col[N][N+1];
bool box[N][N+1];
bool can_fill[N][N][N+1];
int num_can_fill_row[N][N+1];
int num_can_fill_col[N][N+1];
int num_can_fill_box[N][N+1];
int num_can_fill_cell[N][N];
} Sudoku;
num_can_fill_row[r][n] 表示第 r row 有几个格子可填入数字 n ,以此类推
四种角度搜索过程再次统一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#define FILL_IF_EXACTLY_ONE(LOOP1, LOOP2, num_can_fill) \
do { \
LOOP1 { \
if (num_can_fill == 1) { \
LOOP2 { \
if (sudoku_can_fill(thiz, r, c, n)) { \
sudoku_fill(thiz, r, c, n); \
++*num_filled; \
break; \
} \
} \
} else if (num_can_fill == 0) { \
return false; /* pruning */ \
} else if (count_unsolved) { \
++*num_unsolved; \
} \
} \
return true; \
} while (0)
bool sudoku_solve_row(Sudoku *thiz, int *num_filled, int *num_unsolved, bool count_unsolved)
{
FILL_IF_EXACTLY_ONE(
FOR_N(r) FOR_EACH_NUM(n) if(!thiz->row[r][n]),
FOR_N(c),
thiz->num_can_fill_row[r][n]
);
}
bool sudoku_solve_col(Sudoku *thiz, int *num_filled, int *num_unsolved, bool count_unsolved)
{
FILL_IF_EXACTLY_ONE(
FOR_N(c) FOR_EACH_NUM(n) if(!thiz->col[c][n]),
FOR_N(r),
thiz->num_can_fill_col[c][n]
);
}
bool sudoku_solve_box(Sudoku *thiz, int *num_filled, int *num_unsolved, bool count_unsolved)
{
FILL_IF_EXACTLY_ONE(
FOR_N(i) FOR_EACH_NUM(n) if(!thiz->box[i][n]),
FOR_R_C_IN_BOX(r, c, i),
thiz->num_can_fill_box[i][n]
);
}
bool sudoku_solve_cell(Sudoku *thiz, int *num_filled, int *num_unsolved, bool count_unsolved)
{
FILL_IF_EXACTLY_ONE(
FOR_FOR_EACH_EMPTY_CELL(r, c, thiz),
FOR_EACH_NUM(n),
thiz->num_can_fill_cell[r][c]
);
}
更新步骤新增了 FOR_EACH_NUM 的 update,原因是在这之前都不重视已填格子的资讯,但在这版本中已填格子的资讯也变得重要了(某格填入某数后,需要把该格原本的其他可填数设为不可填,因为这会影响该数在该行、列、宫的可填格子个数,反之亦然)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
void sudoku_maybe_update_can_fill(Sudoku *thiz, int r, int c, int n, bool fill)
{
if (fill) {
if (thiz->can_fill[r][c][n]) {
thiz->can_fill[r][c][n] = false;
thiz->num_can_fill_cell[r][c]--;
thiz->num_can_fill_row[r][n]--;
thiz->num_can_fill_col[c][n]--;
thiz->num_can_fill_box[get_box(r, c)][n]--;
}
} else {
if (!thiz->can_fill[r][c][n]
&& sudoku_can_fill_2(thiz, r, c, n)) {
thiz->can_fill[r][c][n] = true;
thiz->num_can_fill_cell[r][c]++;
thiz->num_can_fill_row[r][n]++;
thiz->num_can_fill_col[c][n]++;
thiz->num_can_fill_box[get_box(r, c)][n]++;
}
}
}
void do_sudoku_fill(Sudoku *thiz, int r, int c, int n, bool fill)
{
thiz->grid[r][c] = fill ? n : 0;
const int box_index = get_box(r, c);
thiz->row[r][n] = fill;
thiz->col[c][n] = fill;
thiz->box[box_index][n] = fill;
FOR_N(rr) {
sudoku_maybe_update_can_fill(thiz, rr, c, n, fill);
}
FOR_N(cc) {
sudoku_maybe_update_can_fill(thiz, r, cc, n, fill);
}
FOR_R_C_IN_BOX(rr, cc, box_index) {
sudoku_maybe_update_can_fill(thiz, rr, cc, n, fill);
}
FOR_EACH_NUM(nn) {
sudoku_maybe_update_can_fill(thiz, r, c, nn, fill);
}
}
同样因为这里在意已填格子的状态,需要完善是否可填的定义(检查格子是否为空)
1
2
3
4
5
bool sudoku_can_fill_2(Sudoku *thiz, int r, int c, int n)
{
return !thiz->grid[r][c] && !thiz->row[r][n] &&
!thiz->col[c][n] && !thiz->box[get_box(r,c)][n];
}
最后附上初始化过程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void sudoku_init(Sudoku *thiz)
{
memset(thiz, 0, sizeof(Sudoku));
memset(thiz->can_fill, true, sizeof(thiz->can_fill));
FOR_N(i) {
FOR_N(j) {
thiz->num_can_fill_cell[i][j] = N;
}
FOR_EACH_NUM(n) {
thiz->num_can_fill_row[i][n] = N;
thiz->num_can_fill_col[i][n] = N;
thiz->num_can_fill_box[i][n] = N;
}
}
}
效能分析
方法
每次执行 100×n 次,去除较大较小取其中 60 轮的时间计算平均。(n 随各题计算时间长短做调整,约 1 至 1000 不等)
测资描述
- easy: 简单
- easy_3_ans: 多解
- medium: 中等
- hardest: 号称最难数独,据说是数学家用三个月设计出来的?
不过找一找发现好像有两个版本? - hardest_no_ans: 在上题某空白处填入错误解
| easy | easy_3_ans | |
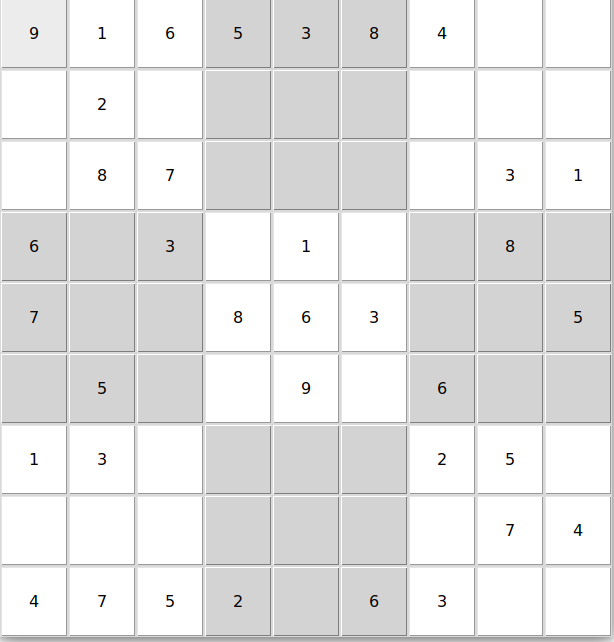 |
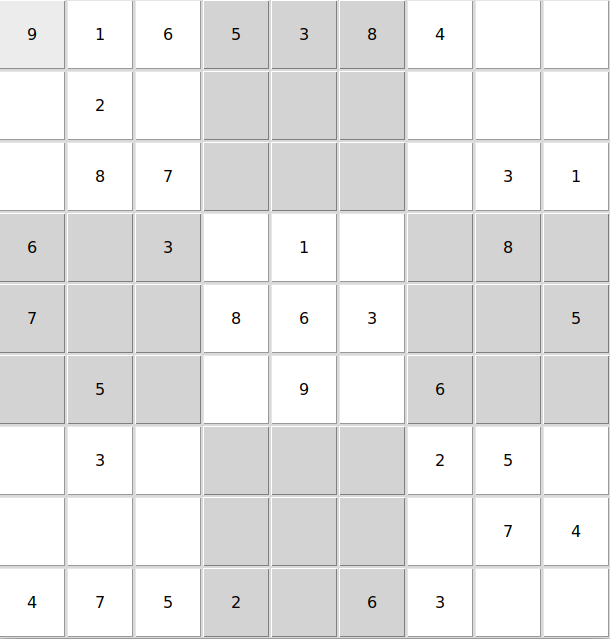 |
|
| medium | hardest | |
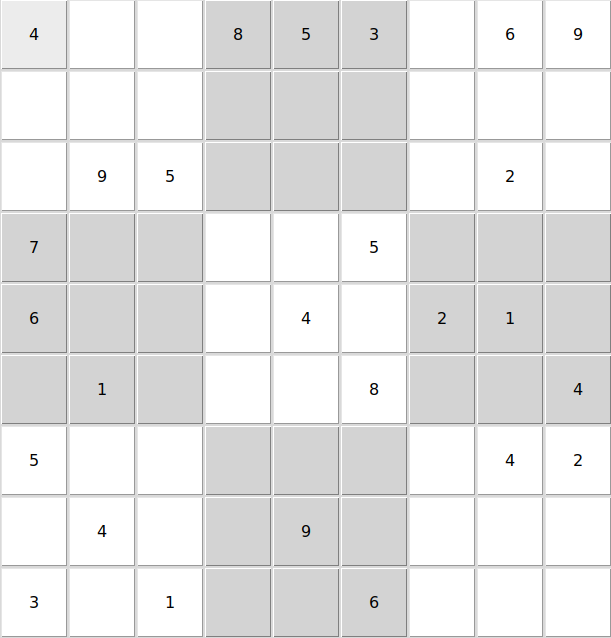 |
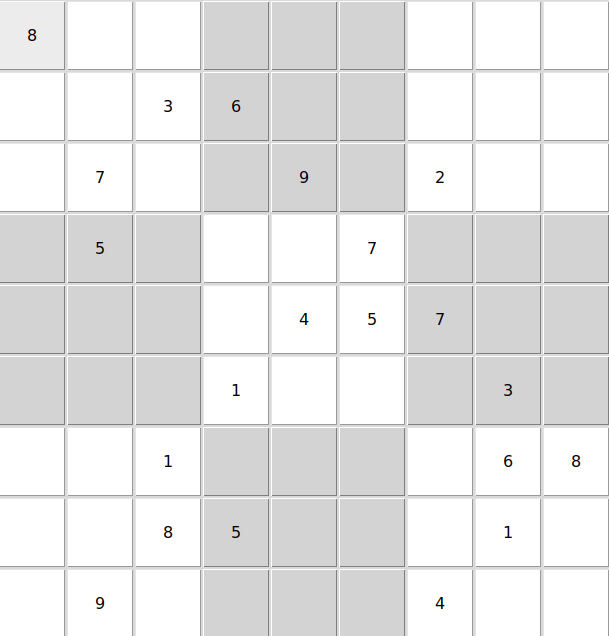 |
|
| hardest_no_ans | ||
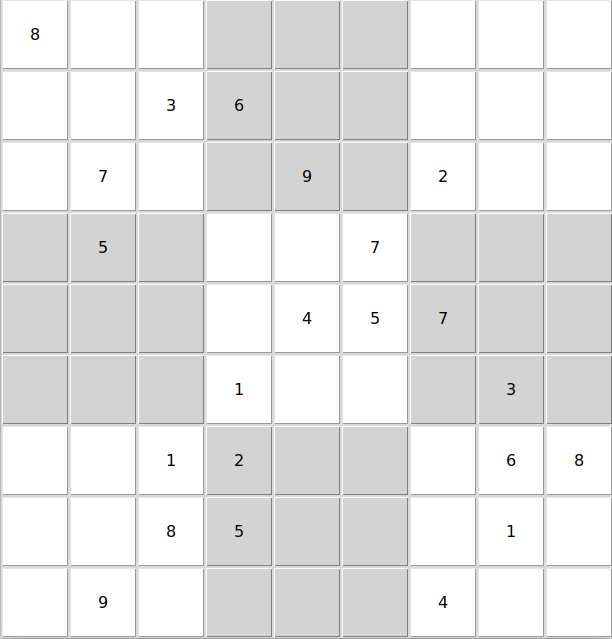 |
结果
解法二和三的优化基本上没 overhead,因此再简单的数独都有明显优化效果
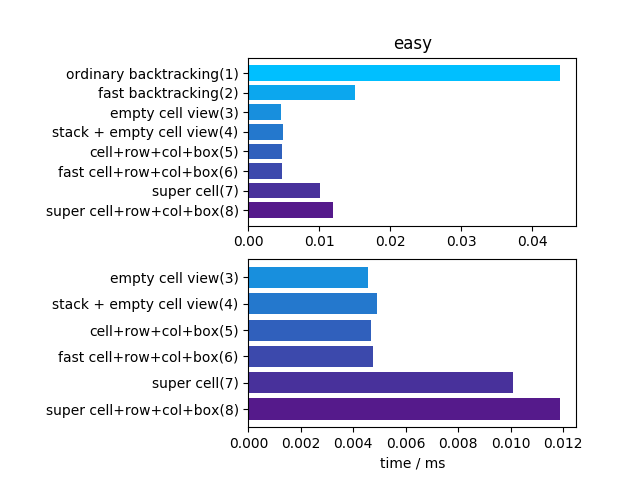
这题更明显地表现出其他解法的 overhead
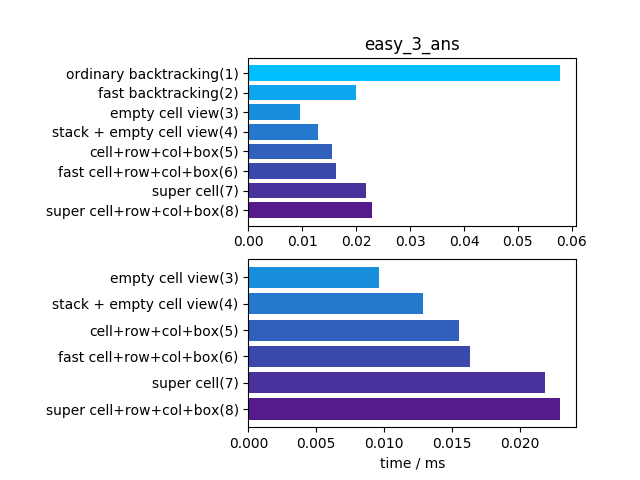
难度稍微提升后差距就明显拉开了
解法四是空间上的优化,不会带来加速
解法六的加速有概率性+少许 overhead,稍微变慢属正常
这题最快的解法八比传统的解法一快了约930倍!
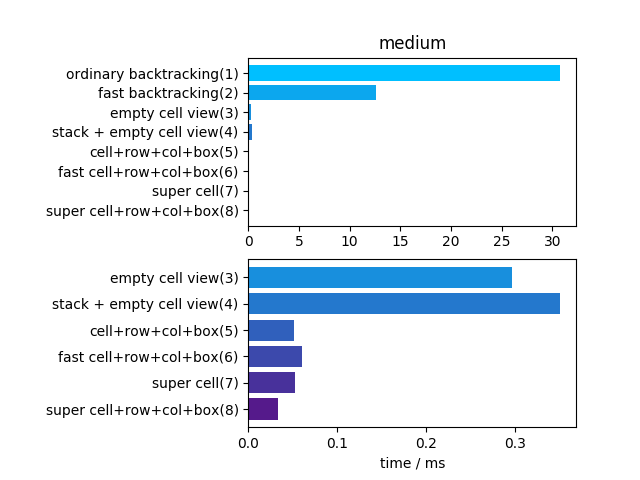
难度提升表示试错次数变多,概率性加速的解法六终于得到充分发挥比解法五快了一倍左右
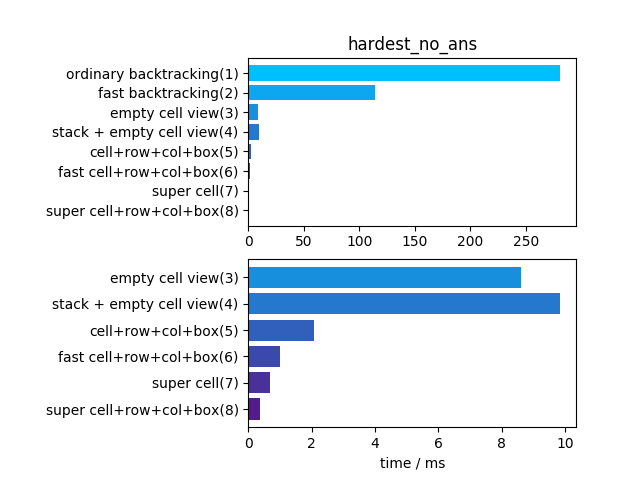
还有最具代表性的数独题
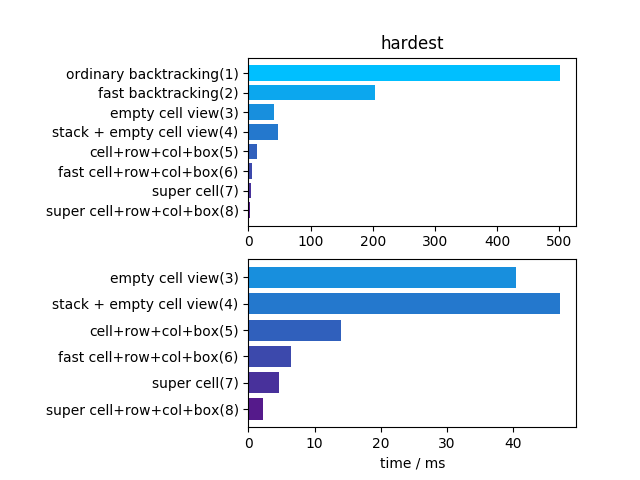
最后是整体时间
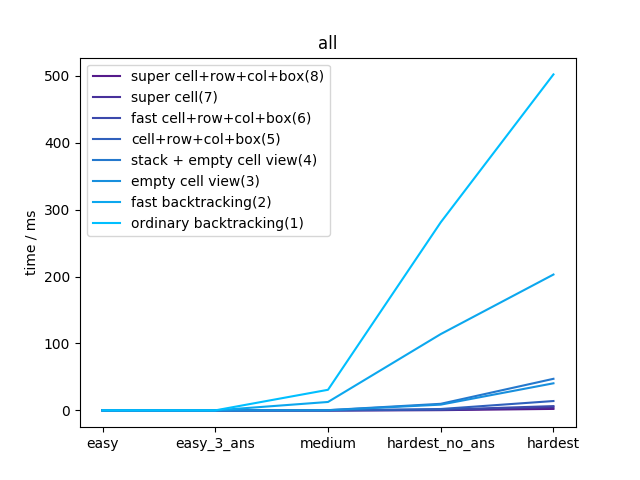
结语
Array 版解法到此告一段落,如有任何问题欢迎在下面留言噢!
如果觉得这篇文对你有帮助,可以到我的 Github repo 点个 star ~
你的小小举动会给我大大的鼓励噢!
补充说明
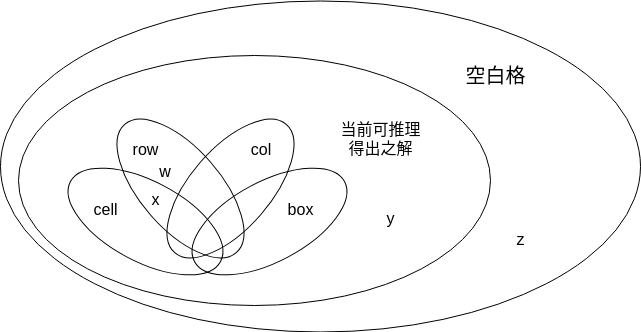
w 只能由 row、不能由 cell 或 col 或 box 观察得出解
x 只能由 row 或 cell 、不能由 col 或 box 观察得出解
y 四种角度都无法观察得出解,但可由推理得知
z 无法由当前情况得出解
 |
 |
|
 |